یعنی اگر ضلعهای یک مثلث را a وb وc بنامیم، همواره خواهیم داشت:
a+b>c
a-b<c
دقت کنید که این قضیه تنها برای مثلث خاصی عنوان نشده است، اگر شما مثلثهای زیادی با اندازههای متفاوت بکشید، میبینید که جمع هر دو ضلع آن از ضلع دیگر بزرگتر و تفاضل هر دو ضلع آن از ضلع سوم کوچکتر است.اما اگر کمی دقت کنید میتوانید تعریف دیگری از این قضیه ارائه دهید. برای راهنمایی فرض کنید میخواهیم از نقطه a به نقطه b برویم.
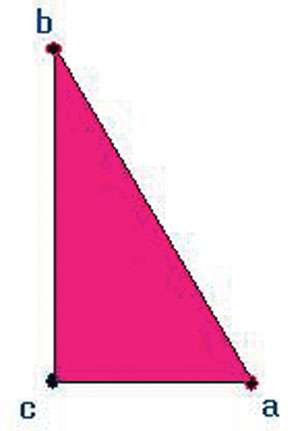
به نظر شما کدام راه کوتاهتر است؟ کاملا واضح است که اگر یکسره از نقطه a به b برویم، مسافت کمتری را نسبت به زمانی که از a به c و سپس به bبرویم طی خواهیم کرد. این دقیقاً معادل همان چیزی است که نامساوی مثلث میگویند. به بیان دیگر کمترین فاصله بین دو نقطه خط راست است. جالب است بدانید که این قضیه به قضیه حمار شهرت دارد. چرا که گفته میشود اگر بوته علفی را در نقطه b قرار دهیم، یک الاغ که در نقطه aقرار دارد، همواره کوتاهترین مسیر را که همان وتر مثلث است برای رسیدن به آن پیش می گیرد!



















